複数の式を作る問題で思考が止まってしまう多くの小学生たち

夏の前半の講習は中間点を過ぎています。

今日の午前中は、受験しない小学生のクラス。夏休み中の学習は既習範囲の復習をしつつ、一歩踏み込んだ問題を演習していくこと。それと、しっかりと式を作っていくことの習慣づけです。

学校の算数の学習は、たとえ文章題題だとしても数字はそのなかに2つしかなく、何となくかけるか割るか足せば答えは出ます。ほとんど問題文を読む必要はないのです。子どもたちはそうしたことに慣れきっているので、式が2つ以上になるととたんにできなくなってしまいます。

たとえば、こんな問題さえもできません。

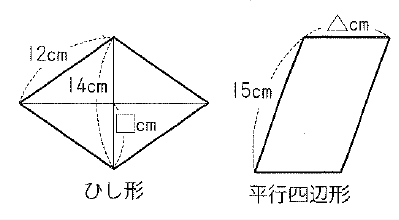
問　まわりの長さが等しいひし形と平行四辺形があります。△の長さを求めなさい。

まず、ひし形の周りの長さを出し(12cm×4)、それと平行四辺形の周りの長さが等しい(48cm)ので、わかっている15cmの2本分(15cm×2)を引いて、2で割れば良いだけです。

(12×4-15×2)÷2

それができないのです。

なぜか?

思考が複数段階になった瞬間に止まってしまうからです。

ふだんから「何も考えずに書かれている数字をかけたり、割ったりして適当に答えを出すこと」に慣れてしまっているので、ちょっとでも考えなければいけない問題になると頭が考えることを停止してしまうのです。そうした小学生は山のようにいます。

そして、ほとんどの保護者の方がそれに気づいていません。

思考力が問われる流れがある中、小学生の現状はこんなものなのです。まずは、算数の問題で、複数の式を立てて解く問題の演習を数多くこなすこと。それが「思考力」へのはじめの一歩です。