2016年神奈川県高校入試問題分析　数学その3

問5　関数についての問題

(ア)　グラフの読み取り　75.7％
(イ)　文章から読み取ってグラフを書く問題　23.6％
(ウ)　方程式をつくってすれ違う時間を求める問題　7.0％

問6　空間図形の問題

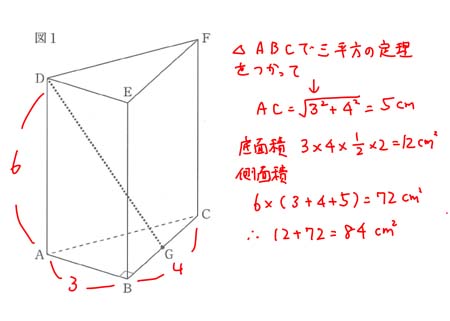
(ア)　展開図から表面積を求める問題　50.1％
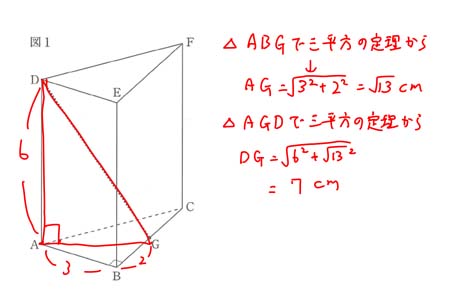
(イ)　三平方の定理を利用して空間の2点の距離を求める問題　54.0％
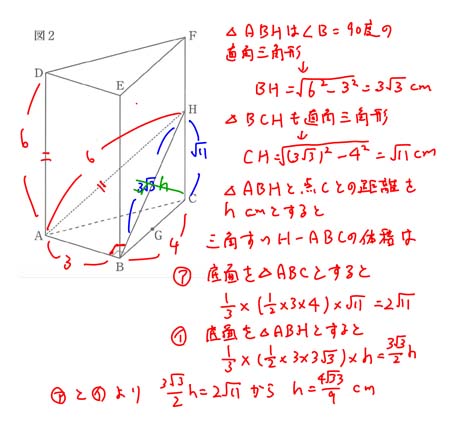
(ウ)　三角形の相似を利用して面と点の距離を求める問題　3.4％

問7　三角形の相似の証明問題　3.5％

問5はH25年まで、神奈川県に特有の二次方程式の応用問題がずっと出題されていました。規則性を読み取り、そこから方程式をたてて解く、というパター化した問題でした。それが、H25年は「式の証明」、H26年に「連立方程式の応用」、H27年「二次方程式の応用」となって、今年は何が出題されるのか予想が分かれるところでした。結果、「グラフの読み取り、グラフの書き、方程式」という出題でした。問題そのものはそれほど難しくはなく、とくに(ア)は正答率も70％をこえています。(イ)と(ウ)についても、時間をかけてじっくり取り組めば出来た生徒も多かったでしょう。いずれにしても、この問5については、来年以降もパターンがないと考えておく必要がある。

予想される出題は、「規則性からの二次方程式or一次方程式の問題」「連立方程式の文章題」「関数の利用をグラフで問う問題」などだ。この問5をふくめて、高校入試に対しては、神奈川県の過去問題だけを解くのではなく、全国の公立高校入試問題を解くようにしておきたい。そうすることで、

問6はいつものように空間図形の出題。ここは年によって難易度がかなり違うのだが、今年は比較的に易しかった。(ア)は下の解説のように三平方の定理で辺ＡＣの長ささえ求められればなんてことのない問題。数字もわかりやすい 3 : 4 : 5 というもの。合格者の半分しかできていないのが残念だ。

(イ)も三平方の定理で辺ＡＧの長ささえ求まれば、もう一度△ＡＧＤで三平方の定理を使うだけ。ここまでやったら(ウ)はとばして先に進んでも良いでしょう。

(ウ)は、そもそも平面と点の距離、という意味がわからなかった生徒も多かったはず。しかも、三角錐の求積を底面の三角形を別にして式を立てて方程式を作る、という発想が浮かばないと解くことが出来ない。正答率が3.4％なのも肯ける問題だ。

問7は図形の証明の問題。Ｈ25年「中点連結定理と平行線の性質から二組の角が等しいことをいい三角形の相似を証明する」　Ｈ26年「円周角の性質を利用して二組の角が等しいことをいい三角形の相似を証明する」　Ｈ27年「円周角の性質を利用して二組の角が等しいことをいい三角形の相似を証明する」と続いてきた。今年も中点連結定理と円周角の性質、平行線の性質を利用しての三角形の相似の証明だったが、完全な解答を書けた生徒はわずか3.5％にすぎなかったようだ。きっと、この前の空間図形の(ウ)にとまどったりと、ここまでくる間に様々に「ひっかかり」をもってしまい、この証明問題に落ち着いて対せなかった、といったところだろう。

数学で８割前後の得点を目指す生徒は、今春の入試問題のように数％の正答率という問題を見きわめ、それ以外の問題をしっかりと得点出来るかが勝負になってくるはずだ。