2016年神奈川県高校入試問題分析　数学その2

前回は、問1と問2で40点の出題があり、それ以下の問題も(ア)については難易度は高くないのでしっかりと得点したい、という話までしました。今回は、問3以降の問題についてです。

問3は「二乗に比例する関数と一次関数の融合問題」です。この問題についてはかなり長いこと同じパターンでの出題がされていて、来春入試でもそれほど大きな変更はないと予想できます。(ア)の正答率が80.5％、(イ)が27.9％、(ウ)が1.9％となっています。この(ウ)が今春数学の入試問題で最も難易度が高かった問題だということです。

入試問題と普段の学校の定期試験との違いは、こうした難易度がとてつもない問題が混じるということです。そのことをしっかりとわかっておいてください。(ウ)の配点は4点です。この問題に長い時間関わってしまい、ここから後ろの問題に手がまわらなかった、といった受験生も多くいたことと思います。大事なことは「見きわめ」です。できれば、このも問題ならば△△分で解ける、といったところまでわかるようにしたいです。

そうなるためには、易しい問題から難しい問題までを解くことです。たくさんの様々な難易度の問題を解くことで、問題を「見きわめる目」を持つことができます。

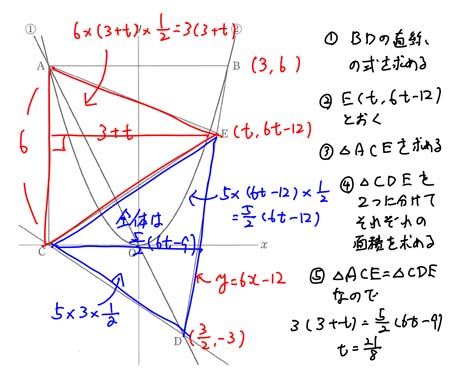
さて、この(ウ)の問題ですが、なにが難しかったのでしょうか。△ACEと△CDEの面積が等しくなる時の点Eの座標を求めなさい、という問題です。ある程度予想はできる問題で、miyajukuでも入試前にたくさんの類題を解いています。この場合は、等積変形を使うか、実際に面積を出して等しい関係で方程式を作るか、といった2パターンです。下の図に解き方の流れを書き出しました。計算もそれほど面倒ではなく、解けなかった生徒も、後で冷静にと解き直したら「できた」となったはずでしょう。発想としてはE点のX座標を何らかの文字でおけたか、といったところでしょう。そこさえクリアできれば、あとはスムーズに解けたはずです。とはいっても、解答を導くまでの工程が多く、ちょっとつまずくとイライラしてきそうです。問3で頭に血を上らせては、以下の問題に影響します。

問4は「確率」の問題でした。昨年は「統計」の出題でした。長い間、この問4には「確率」の問題が出題されていて、昨年は突如として変更になり、今年はどうなるのかなぁ、と思っていたらもとに戻ったということです。ただ、来年の出題も「確率」とは限りません。ここには「統計」や「確率」などの「資料の活用」の問題が出題されると考えて準備をしておきましょう。そうした意味では、パターンがなくなっているのが県入試の特長です。正答率は、(ア)が68.7％で、(イ)が14.4％、(ウ)が15,2％と難しかったようです。

この(イ)と(ウ)の問題も、確率の問題であると同時に、中1の平面図形、中2の三角形と四角形、中3の円周角と中心角の知識が融合した問題になっています。さらに、問題をしっかりと読解するチカラも求められます。きちんと整理整頓しながら求める場合の数を数えていく。そんな作業をしっかりとできるかどうか。そんなチカラが求められています。表を書きながら「数え忘れ」がでないように注意して解くべきです。数学が不得意な生徒でも、確率の問題はある程度の「根性」があれば解けることもあります。数学が不得手な生徒は、問1と問2のあとは、この問4を解くようにするといいでしょう。

問5以下についてはまた次回。