14年度入試分析と15年度入試の予想　その3

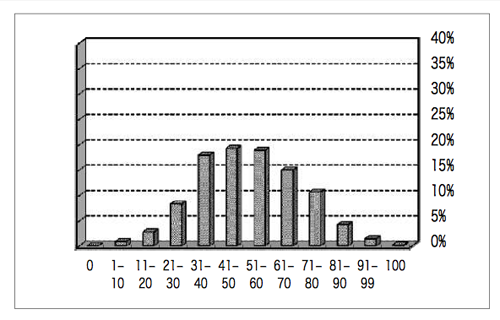
まずは得点分布です。

きれいな正規分布ですね。ある意味ではこの得点分布が数学の特長です。問題の難易度がサービス問題から正解率が数％のものまでバラエティに富んで出題されている、ということです。したがって、自分の数学のチカラをしっかりと見きわめ、できる問題をしっかりと得点すること、数学に対する対策はそれにつきます。

どの問題が易しいかというと、問1と問2です。問1の計算問題は基本的な出題しかされません。問2は様々な分野から出題されますが、教科書の例題レベルです。正解率も80％前後です(1問だけ7％でしたが)。ここまでは何があっても全問正解したいです。

その他の問題は一昨年に比べると「ひとひねり」された出題が増えました。また、確率の問題で図や例が省かれるなど、自分で問題の内容を読み取らねばならない出題も増えました。大切なのは「見きわめる目」を持つことです。できない問題に何分も時間をかけるのでなく、できる問題をしっかりと解くことです。その「見きわめ」こそが重要です。

関数の問題など線がたくさんあって難しく見えます。しかし、これらの線は「こけおどし」です。問題を解くのに必要な情報はその一部です。図形の証明問題も昨年から完全証明にかわって難しくなったように思われがちですが、実は内容はたいしたことはありません。すべて書くのはなぁ、などと思わずにしっかりと得点をかせぎましょう。

逆に今年の問題の中で最も面倒だった2問。問5の連立方程式と問6(ゥ)の三平方の定理の問題。それぞれ正答率は3.7％と1.8％でした。こうした問題は数学が得意でない生徒は手を出さないで良いです。時間をかけるだけムダになります。また、来年の入試で同じパターンの問題が出題されるかもわかりません。出題の非パターン化というのもここのところの数学の出題の特長です。連立方程式を一所懸命に学習しても、来年度入試で出題はなかった、ということも十分に予想されます。

まとめますと、数学については自分の目標点を定め、その得点をどの問題でとるのかをしっかりと決めた学習を進めていくことです。